Learning how to code is difficult enough as it is, so there’s no need to make it harder than necessary
One of the easiest ways to learn programming faster is to start with the easiest programming language you can find.
After all, any programming language is simply a tool to build something useful with code. Learning the language isn’t the goal per se, right?
As it turns out, you can use a handful of practical ways to find the easiest programming language to learn.
That way, you will spend less time trying to understand and troubleshoot the language and your code. That gives you more time to build something meaningful to practice your skills.
In this post, I’ll walk you through a few practical ways to find out which programming languages are relatively easy to learn.
Also, based on our findings, we’ll look at four programming languages that are easy for beginners.
If you have never learned programming before, this post will help you find the easiest programming language to get started.
Keep reading!
Here are a few related posts you might want to read:
- How to Start Learning Coding? 6 Time-Saving Tips for Beginners
- 10 Misleading Coding Myths You Should Ignore
- How Computer Science Basics Can Help You Learn Coding Faster
Please note: This post contains affiliate links to products I use and recommend. I may receive a small commission if you purchase through one of my links, at no additional cost to you. Thank you for your support!
What programming language should I learn in 2023?
Choosing a programming language to learn may feel overwhelming.
Especially if you’re just starting out with learning how to code, it’s easy to feel intimidated by dozens of options to choose from.
But the truth is:
It doesn’t matter which programming language you learn.
The most important thing is that you start, that’s all.
Although you might want to find the easiest programming language to learn, remember that every language is simply a tool to create something useful. In other words, the first thing you should figure out is this:
What do I want to build and achieve with coding?
When you know what you want to create, you can narrow down your options to just a handful of programming languages.
Then, you can use the points in this article to find the easiest programming language in that bunch.
Related: 4 Must-Have Skills to Become a Front-End Web Developer
Thus, if you’re choosing your first programming language to learn, take this article with a grain of salt. Don’t start learning a language simply because it’s listed among the easiest ones to learn.
Instead, start by setting yourself a long-term goal:
- What made you interested in learning to code in the first place?
- Did you have an idea for a project you want to build?
Then, see what options you have. As I said above, each language is a tool for building something useful – just like any tool in the toolbox.
If you want to cut through wood, you’d use the saw and not the hammer, right? (Even if the hammer might be easier to use or more popular.)
In a similar way, if you want to learn programming to build websites or analyze data, don’t choose a language used for developing desktop applications only.
For a more thorough article on what programming language to learn, check out my previous post: Which Programming Language Should I Learn? Beginner’s Guide.

What makes a programming language easy?
What makes a programming language “easy”?
How can you find the best programming language for beginners?
While some programming languages may boast a beginner-friendly syntax that reads a lot like English, it might be offset by other factors that make learning it relatively difficult.
Therefore, you should consider a handful of factors when trying to find the easiest programming language to learn.
In this post, we’ll go through three helpful points to help you find a programming language that is relatively easy to learn:
Let’s start by looking at the ease of learning and using a specific programming language:
1: Ease of learning and using
When you’re learning to code, learning any programming language isn’t a goal for you per se.
Instead, any given language is your tool for building something useful with code, right?
That being said, you want to find a programming language that’s relatively easy to learn and use.
You don’t want to waste your time trying to figure out how the language itself works. Instead, you want to focus on learning how programming works and how you can use it to solve problems.
Related: 14 Different Programming Languages and Their Uses Explained
Now, every programming language has a set of rules and grammar it follows. That’s called the syntax and it’s the first thing you see when you look at code written in a certain language.
When it comes to how easy a programming language is to learn, the syntax often plays a big role.
While some programming languages read a lot like English, others are more cryptic and complex to write and read.
Low-level vs high level programming languages
What sets different languages apart in this sense is whether they are high-level or low-level programming languages:
- Low-level programming languages are generally harder to read. They are closer to machine code (consisting of just 1’s and 0’s), making them relatively difficult for beginners to learn.
- High-level programming languages use natural language in their syntax, making them easier to read and write.
Summing it up: the biggest advantage of high-level languages is that you will spend less time trying to understand how the language itself works.
Thus, you can use more time learning programming and how to solve problems and build useful, fun projects for your portfolio.
Related: 17 Programming Language Paradigm Terms Explained
Examples of high-level programming languages
Here are a few powerful high-level programming languages that are relatively easy to learn for beginners:
- Python:
One of the most popular programming languages worldwide. Extremely powerful, versatile, and easy to learn. Check out these advantages of Python over other programming languages to see what I mean. - Ruby:
Quick to learn in terms of syntax. Used mainly for creating web applications – very popular among startups to get web apps up and running quickly. - JavaScript:
Popular, powerful, and versatile – JavaScript is everywhere these days. Used for both front-end and back-end web development. One of the best tools to learn if you want to build web-based projects. - Java:
Popular across (almost) all platforms, operating systems, and devices. Great for a bunch of projects from Android mobile apps to desktop software. - PHP:
Although not the easiest or sexiest language to learn, PHP is wort mentioning if you want to become a freelance Web Developer. It powers WordPress, the most popular Content Management System worldwide, which is a huge platform for making money either by building websites for clients or by creating and selling paid themes and plugins.
Recommended: The Best Programming Languages for Web Development in 2023 (And Beyond)
2: Availability of learning resources
Now that we know which languages read easier than others, let’s think about the next factor: availability of learning resources.
After all, if you can’t find tutorials, online courses, or books that help you learn the language faster, you’ll have less time to dedicate to actually learning how to use the language for programming.
As a rule of thumb:
You’ll find more learning resources for the most popular programming languages. The more people are interested in learning it, the more helpful content will be produced – mainly online coding courses or programming books.
Finding the best learning resources
Luckily, nowadays you can find heaps of online courses, tutorials, and books for almost any programming language out there. In fact, what’s more of a challenge is to find the ones that help you learn coding fast.
Therefore, the first thing you should know is this:
What types of learning resources help you learn the best?
In other words: Be aware of how you learn the fastest. If you like having a book in your hand, get a book with great reviews to learn the language of your choice.
And if you learn better by listening and watching, use online coding courses with video tutorials.
If you’re not sure which learning resources to use, check out my post on Online Coding Courses vs. Programming Books: Which One Should You Use?
Where to start looking?
Here are a few resources you can find and use to support your learning:
- Official language documentation:
Written by the developers and contributors. Helpful for getting familiar with how to use a language to solve specific problems. - Free online courses:
Use free learning resources to get a first impression and see if you enjoy working with a certain programming language. - Comprehensive books:
Look for beginner-friendly books with the best reviews, something that’s helpful to have for any future reference. - Paid online courses:
Most paid courses come with helpful projects where you can practice using the language for real-world programs. Great for hands-on practice to get an idea what to use the language for. Just remember to take breaks from online lectures to build something on your own. - Active discussion forums:
The more popular a certain language is, the more likely it is that someone has already asked a question you’re struggling with before (most likely on Stack Overflow).
Related: The Best Websites to Learn Coding in 2023
The best way to practice and learn programming fast
Whatever method you choose, keep in mind that the best way to learn a programming language is to use it for your own projects.
Therefore, make sure you practice a lot on your own – without the help from your book or online course.
Thus, while you’re learning, put everything in your own words by taking notes.
Then, build your own programs just by using your notes. If you’re struggling with a specific topic, go back to your book or online course for a quick refresher.
This will help you notice what areas you still need more practice in. Following books and online courses by repeating the exercises is one thing, but knowing how to use those concepts to build something by yourself is your goal with everything you learn.
Related: The Best Way to Learn How to Code: Beginner’s Guide
3: Size of community
By now we know that both the readability of a given language as well as the availability of learning resources will help you find the easiest programming language to learn.
Next, let’s consider how the size of the community around a certain language affects how easy it is to learn.
In short: When heaps of people around the world are using a programming language, the large community has a few key advantages.
First, the more developers are using a certain language, the easier it is to find help.
Thus, whenever you run into a problem while trying to solve a problem with code, you can head online. Simply type your problem into Google and hit Enter.
The quicker you find an answer to your question, the more time you can dedicate to actually learning the language and building projects with it.
Second, a big community means a relatively bigger job market with employment opportunities.
The more developers use a language at work, the more jobs there must be for that language.
Related: How to Make Money Coding? 12 Popular Way to Earn Money as a Developer
Thus, let’s look at three different measures for community size and popularity:
Measure #1: Popularity among developers
There are a few practical ways to find out the community size around a specific programming language.
Let’s start by looking which programming languages are the most commonly used in the developer community as a whole.
The Stack Overflow Survey is a good place to start.
Here’s an overview of which programming, scripting, and markup languages the respondents are using:
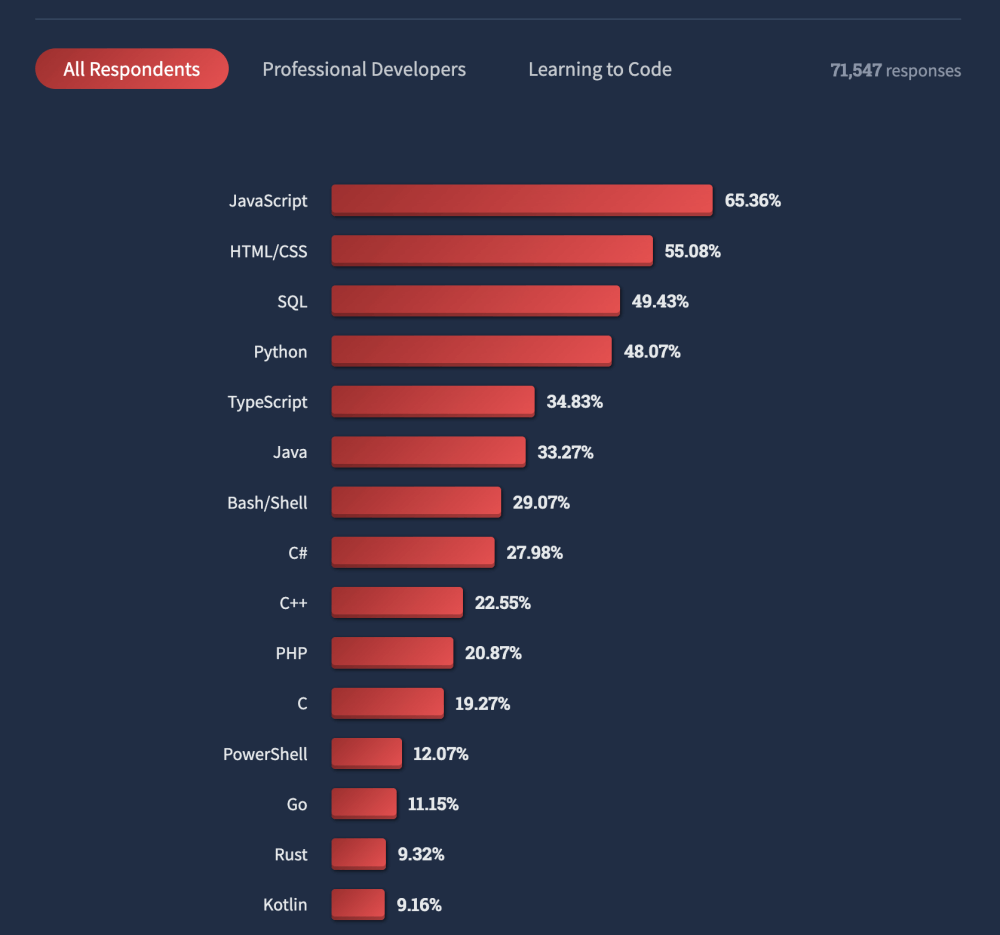
The first thing we see is that the top languages with the biggest shares of developers using them are used for web-based projects.
Most of the over 71,000 respondents work with front-end development languages on the client-side:
They are followed by SQL – a popular language for database management – and back-end development languages like Python, Typescript, Java, Bash/Shell, and C#.
Measure #2: Popularity on discussion forums
Next, let’s consider how easily you can find answers to coding-related questions online.
Stack Overflow is the biggest platform connecting developers around the world. The discussion threads there are some of the best resources to find answers to your questions about a programming, scripting, or markup language.
Here are the most popular languages in terms of tagged active discussion threads:
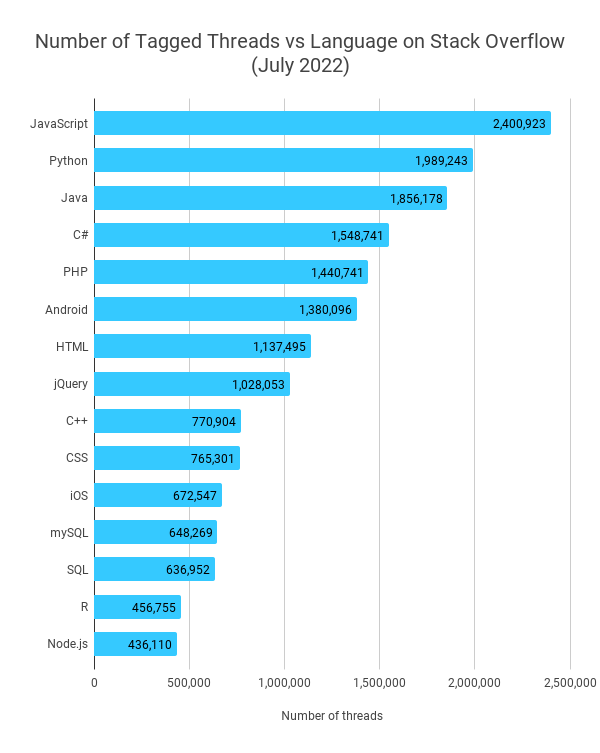
The top eight languages and skills have a clear lead with over 1 million active threads each. With such a gigantic database of questions and answers, it’s very likely that someone has already asked any questions you might have while learning.
If that’s the case, troubleshooting your code will be easy and fast. When you need help, you don’t have to start a new thread and wait for others to answer your question.
Measure #3: Popularity in open-source projects
As a third source, let’s see which are the most popular programming languages used for projects on GitHub.
What makes GitHub so helpful for learning is that you can read other people’s code. It’s the best way to find new ideas for solving problems and thinking outside the box.
Here are the most common languages used for projects in GitHub repositories in 2014-2022:
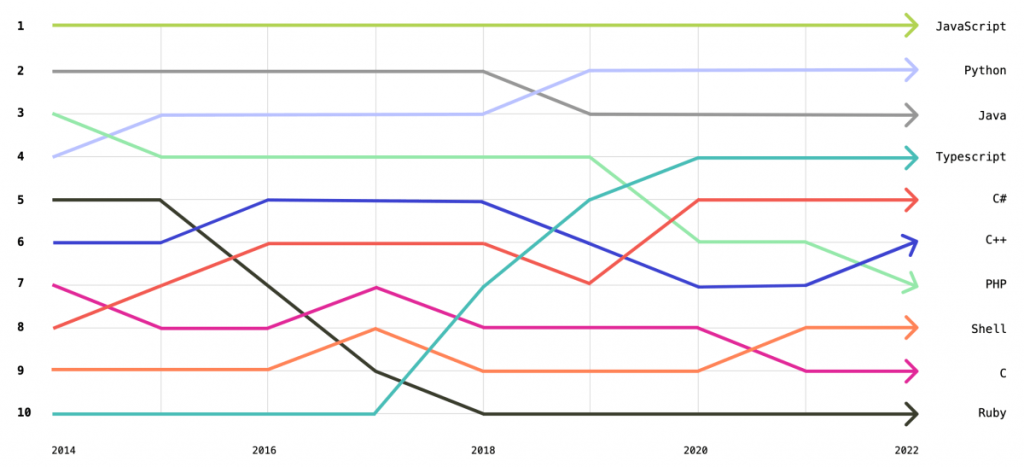
Again, we see familiar languages like JavaScript, Python, Java, Typescript, and C# in the top spots.
As for the trend over the past few years, all of them seem to hold their positions close to the top of the list.
Summing it up: The easiest programming languages in terms of community size
Based on programming language popularity, we see that the easiest programming language to learn would be one of these:
- JavaScript
- Python
- Java
- C#
- C++
- PHP
In short: if you choose to learn one of these languages, you can find help easily whenever you have a question.
Therefore, these programming languages are easy for beginners because you can focus on learning and practising instead of troubleshooting.
Related: 10 Powerful Tips to Learn Coding Faster
Next up: Easiest programming languages for beginners in 2023
Now we know which programming languages are easy to learn, have helpful learning resources available, and boast a big global community to support your learning.
Putting it all together, here are the easiest programming languages for beginners in 2023:
- JavaScript
JavaScript is must-have tool if you want to become a web developer. You can use popular frameworks to get your project on its feet faster, like Angular, React, or Ember. Check out the best way to learn JavaScript to get started. - Python
Python has gained worldwide popularity faster than any of the other big languages. Python has a clear syntax that reads much like English, so it’s perfect for absolute beginners. Start with these best YouTube tutorials to learn Python. - Ruby
Ruby is a powerful tool for building dynamic web applications. With the Ruby on Rails framework, you have a clean, easy-to-learn language under your belt. - Java
Java holds a consistent place among the most popular programming languages. It is a valuable skill to learn if you want to start a career as a back-end developer. Thanks to its popularity, you’ll find lots of resources to support your learning.
Now head over to my post on top programming languages for beginners to find the best free online courses to start learning today!
Final thoughts: The easiest programming language for beginners in 2023
Learning how to code is difficult and it takes a lot of hard work to become a professional developer.
Thus, one of the best ways to speed things up is to find the easiest programming language to learn.
Here is a quick overview of the points you should consider when you’re looking for an easy to learn language:
- Choose a high-level programming language:
High-level languages have a more beginner-friendly syntax. The code easier to read, write, and manage. - Check the availability of learning resources:
Make sure you can find helpful resources to support your learning: official documentations, free and paid online courses, books, etc. - Look at the size of the community:
Choose a programming language that has a large and supportive global community. The more developers are using it, the more likely it is that you’ll find answers to whatever questions you may have relatively fast.
How would you go about finding the easiest programming language to learn? Share your thoughts in the comments below!
When you’ve found an easy to learn programming language, check out my post with the best websites to learn coding to start learning!
Here are a few related posts you might want to read:
- 5 Top Web Development Courses for Beginners
- How to Choose an Online Course and Get Your Money’s Worth
- 10 Simple Reasons Why You Should Start an Online Coding Course
If you liked this article about the easiest programming language to learn, just drop me a line in the comments below!
P.S. If you found this post helpful, please share it with others! Thanks!
Happy coding!
– Mikke


